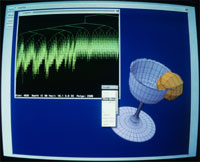
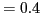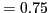- Real-Time Graphics |
- Rendering |
- Animation |
- Geometric Modeling |
- Scientific Visualization |
- Software System

- On Using Curvature Characteristics for Polygonal Models

- Low Degree Approximation of Surfaces for Revolved Objects

- Higher Order Interpolation and Least-Squares Approximation Using Implicit Algebraic Surfaces

- Smoothing Polyhedra using Implicit Algebraic Splines

- Algebraic Surface Design with Hermite Interpolation

- Piecewise Linear Approximations of Digitized Space curves with Applications

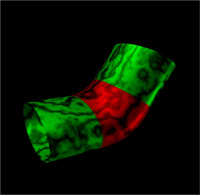
This paper presents two measures that approximate surface curvature. The first measure, which can be proven to converge to the exact Gaussian curvature as we take finer polygonization, estimates the Gaussian curvature of various polygonal surfaces. This measure is geared up in an attempt to extract and visualize shape characteristics of polygonal surfaces and is shown to work effectively when exact mathematical equations of original surfaces are not known or are computationally expensive to handle. The second measure, although not so mathematically sound as the first one, is appropriate for an algorithmic process of adaptive polygonization. While it finds out easily how much a surface region bends, this measure is free of the intrinsic problems arisen in the Gaussian or mean curvatures. We adopt this measure in our new physically-based mesh generation algorithm that produces adaptively relaxed triangular meshes for parametric surfaces.
- I. Ihm, T. Park, Y. C. Wee, and S. Y. Shin, "On Using Curvature Characteristics for Polygonal Models", Computer Graphics International '94, pp.267-278, Melbourne, Australia, June 1994.
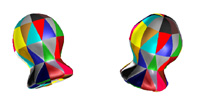
- Examples of the display of Gaussian curvature, approximated from the respective polygonized models

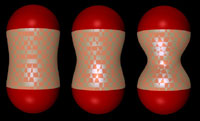
We present a method for generating low degree 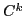 -continuous piecewise algebraic surfaces for revolved objects. The approximating pieces are implicitly defined algebraic surfaces whose profile curves can be obtained algebraically or parametrically from digitized points. We show that degree
-continuous piecewise algebraic surfaces for revolved objects. The approximating pieces are implicitly defined algebraic surfaces whose profile curves can be obtained algebraically or parametrically from digitized points. We show that degree 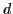 surface patches can be used for approximations with inter-patch
surface patches can be used for approximations with inter-patch 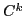 continuity as high as
continuity as high as 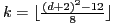 for even
for even 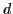 , and
, and 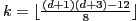 for odd
for odd 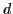 . As an example, we construct
. As an example, we construct 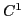 cubic surfaces and
cubic surfaces and 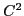 quartic surfaces for revolved objects from digitized profile curves.
quartic surfaces for revolved objects from digitized profile curves.
- C. Bajaj, and I. Ihm, "Lower Degree Approximation of Surfaces for Revolved Objects", Graphics Interface '93, pp.33-41, Toronto, Canada, May 1993.
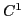 cubic and
cubic and 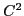 quartic revolved surface models.
quartic revolved surface models.
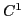 cubic and
cubic and 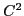 sextic revolved surface models.
sextic revolved surface models.

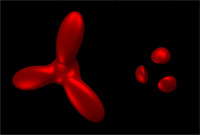
In this paper, we characterize the solution space of low degree, implicitly defined, algebraic surfaces which interpolate and/or least-squares approximate a collection of scattered point and curve data in three dimensional space. The problem of higher order interpolation and least-squares approximation with algebraic surfaces under a proper normalization reduces to a quadratic minimization problem with elegant and easily expressible solutions. We have implemented our algebraic surface fitting algorithms, and included them in the collaborative distributed geometric environment SHASTRA. Several examples are given to illustrate how our algorithms are applied to algebraic surface design.
- C. Bajaj, I. Ihm, and J. Warren, "Higher-Order Interpolation and Least-Squares Approximation Using Implicit Algebraic Surfaces," ACM Transactions on Graphics, Vol. 12, No. 4, pp. 327-347, October 1993.
- A
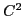 continuous algebraic surface family of blobs.
continuous algebraic surface family of blobs.
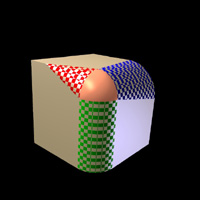
- Corner blending with algebraic surfaces.
- SHILP: an algebraic surface editing tool.

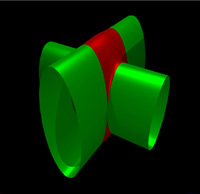
Polyhedron "smoothing" is an efficient construction scheme for generating complex boundary models of solid physical objects. This paper presents efficient algorithms for generating families of curved solid objects with boundary topology related to an input polyhedron. Individual faces of a polyhedron are replaced by low degree implicit algebraic surface patches with local support. These quintic patches replace the 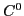 contacts of planar facets with
contacts of planar facets with 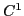 continuity along all interpatch boundaries. Selection of suitable instances of implicit surfaces as well as local control of the individual surface patches are achieved via simultaneous interpolation and weighted least-squares approximation.
continuity along all interpatch boundaries. Selection of suitable instances of implicit surfaces as well as local control of the individual surface patches are achieved via simultaneous interpolation and weighted least-squares approximation.
- C. Bajaj, and I. Ihm, "Smoothing Polyhedra Using Implicit Algebraic Splines", Computer Graphics (ACM SIGGRAPH '92), Vol. 26, No. 2, pp. 79-88, Chicago, U.S.A., July 1992.
- Smoothing a convex polyhedron
- Smoothing a non-convex polyhedron with quintic algebraic patches
- Two quintic algebraic patches with different
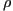 values
values
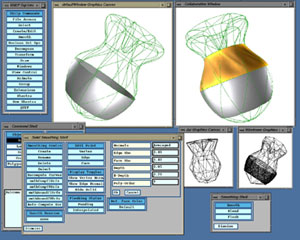
- A polyhedron smoothed in the SHASTRA Distributed and Collaborative Geometric Design Environment

This paper presents an efficient algorithm, called Hermite interpolation, for constructing low degree algebraic surfaces, which contain, with 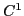 or tangent plane continuity, any given collection of points and algebraic space curves having derivative information. Positional as well as derivative constraints on an implicitly defined algebraic surface are translated into a homogeneous linear system, where the unknowns are the coefficients of the polynomial defining the algebraic surface. Computational details of the Hermite interpolation algorithm are presented along with several illustrative applications of the interpolation technique to construction of joining or blending surfaces for solid models as well as fleshing surfaces for curved wire frame models. A heuristic approach to interactive shape control of implicit algebraic surfaces is also given, and open problems in algebraic surface design are discussed.
or tangent plane continuity, any given collection of points and algebraic space curves having derivative information. Positional as well as derivative constraints on an implicitly defined algebraic surface are translated into a homogeneous linear system, where the unknowns are the coefficients of the polynomial defining the algebraic surface. Computational details of the Hermite interpolation algorithm are presented along with several illustrative applications of the interpolation technique to construction of joining or blending surfaces for solid models as well as fleshing surfaces for curved wire frame models. A heuristic approach to interactive shape control of implicit algebraic surfaces is also given, and open problems in algebraic surface design are discussed.
- C. Bajaj, and I. Ihm, "Algebraic Surface Design with Hermite Interpolation", ACM Transactions on Graphics, Vol. 11, No. 1, pp. 61-91, January 1992.
- C. Bajaj, and I. Ihm, "Hermite Interpolation Using Real Algebraic Surfaces," The Fifth Annual ACM Symposium on Computational Geometry, 94-103, Saarbruchen, W. Germany, June 1989.
- Smooth joining of two cylinders with a cubic surface.
- Smooth joining of three cylinders with a quartic surface.
- "Good" and "bad" quartic joining surfaces.
- Smooth joining of four cylinders with a quartic surface.
- Smooth blending of two cylinders with a quartic surface.
- Smooth blending of two cylinders with a quartic surface.
- Smooth fleshing of a wire frame with quadric and quartic surfaces.
- Interactive shape control using barycentric coordinates.

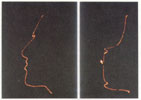
Generating piecewise linear approximations of digitized or densely-sampled curves is an important problem in many areas. Here, we consider how to approximate an arbitrary digitized 3-D space curve, made of 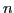 points, with
points, with 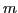 line segments. We present an
line segments. We present an 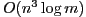 time,
time, 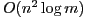 space, dynamic programming algorithm which finds an optimal approximation. We then introduce an iterative heuristic algorithm, based upon the notions of curve length and spherical image, which quickly computes a good approximation of a space curve in
space, dynamic programming algorithm which finds an optimal approximation. We then introduce an iterative heuristic algorithm, based upon the notions of curve length and spherical image, which quickly computes a good approximation of a space curve in 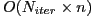 time and
time and 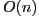 space. We apply this fast heuristic algorithm to display space curve segments and implicit surface patches, and to linearly approximate curved 3D objects, made by rotational sweeping, by binary space partitioning trees that are well-balanced.
space. We apply this fast heuristic algorithm to display space curve segments and implicit surface patches, and to linearly approximate curved 3D objects, made by rotational sweeping, by binary space partitioning trees that are well-balanced.
- I. Ihm, and B. Naylor, "Piecewise Linear Approximations of Digitized Space curves with Applications", Computer Graphics International '91, pp.545-569, Boston, U.S.A., June 1991.
- Examples of the heuristic subdivision
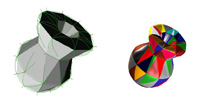
- Building a BSPT model of a goblet, partitioned through the heuristic subdivision method



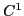 and
and 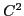 -continuous goblets
-continuous goblets